What is the radius of the earth?

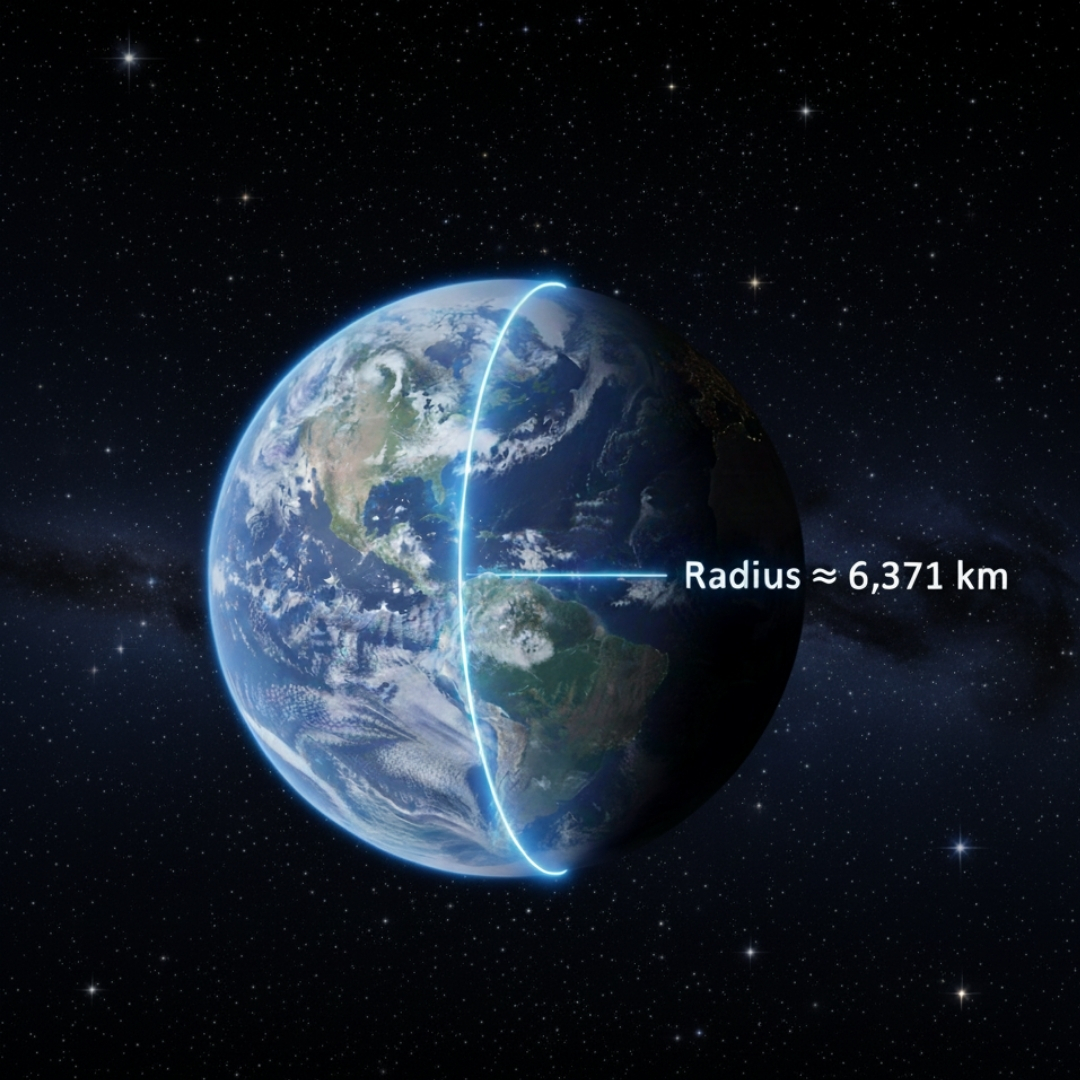
The Earth's radius is a key boundary that assumes a critical role in different logical estimations and understandings of our planet. The typical radius p of the Earth is around 6,371 kilometers (3,959 miles). In any case, it's vital to take note that the Earth is certainly not an ideal circle but rather an oblate spheroid, meaning it is marginally straightened at the posts and protruding at the equator.

 

The assurance of the Earth's radius is a consequence of hundreds of years of logical requests and estimations. Early Greek scholars and mathematicians, for example, Eratosthenes, made critical commitments to assessing the Earth's radius. Eratosthenes, in the third century BCE, utilized straightforward calculation and perceptions of the sun's point at two unique areas to assess the world's periphery, from which the sweep could be determined.

 

 

Present-day estimations of the Earth's radius include advanced methods, for example, satellite perceptions, radar running, and global positioning systems (GPS). Satellites in a circle around the Earth can unequivocally quantify the separation from their situation to the world's surface, considering exact estimations of the world's shape and aspects.

 

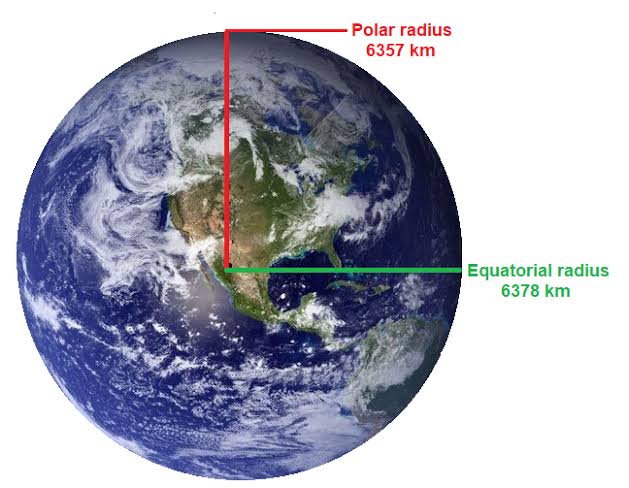
The Earth's equatorial radius is somewhat bigger than its polar span because of its oblate spheroid shape. The central range is around 6,378 kilometers (3,963 miles), while the polar span is around 6,357 kilometers (3,949 miles). The distinction between these two qualities mirrors the smoothing at the posts and swelling at the equator.

 

The Earth's radius is a critical boundary in various logical disciplines, including geophysics, stargazing, and map-making. In geophysics, information on the world's span is critical for grasping gravitational powers and the appropriation of mass inside the planet. Stargazers utilize the Earth's radius as a source of perspective while concentrating on heavenly bodies and computing distances in the universe.

 

In map-making, the Earth's radius is crucial for making precise guides and addressing the world's surface in a two-layered design. Different guide projections represent the world's curve in different ways, and the exact estimation of the earth's radius adds to more exact planning.

 

Understanding the Earth's radius isn't just significant for logical examination; in addition, it has functional ramifications in fields like route, satellite correspondence, and space investigation. Exact information on the world's aspects takes into account the improvement of innovations that depend on exact computations connected with the planet's size and shape.

 

In outline, the Earth's radius is a fundamental boundary in logical exploration and mechanical applications. Progresses in estimation strategies and logical comprehension have prompted a more precise assurance of the world's span, giving an establishment to a great many logical and reasonable undertakings.

 

The radius of the Earth is a basic measurement that has great significance in various scientific endeavors from understanding the structure of our planet to aiding in navigation and satellite communication. The Earth’s radius is defined as the distance between its center and its surface, and it is approximately 6,371 km (3,959 miles). This value represents the average value for radius since the earth is not a perfect ball but rather an oblate spheroid; this means that owing to spinning rotation, it becomes flattened at poles and bulges at the equator. This difference in radii is quite small with the polar radius being 21 km (13 mi) less than the equatorial radius.

The quest for determining Earth’s radius dates back many centuries ago. Ancient Greek intellectuals were among the first individuals who measured it using geometry techniques and observations of celestial objects. However, more accurate measurements were only achieved in modern times when technology and mathematics improved. For example, Satellite-based geodesy systems like Global Positioning Systems (GPS) have made it possible for very precise computations of Earth’s shape and diameter.

 

The Earth’s radius does not just serve curiosity in science but also comes in handy in practical applications.
In addition, the radius of Earth is an important factor in navigation systems. It is important to know the size and shape of the earth whether by air, sea, or land to be able to determine positions and distances accurately. GPS uses this precise measurement of Earth’s radius with high precision for position calculation on any point of the planet.

Also, knowing the earth’s radius helps us understand planetary science and beyond. By examining its size and make-up, scientists can compare these with other heavenly bodies; thus generating explanations on how planets came into being and matured.

To sum up, Earth’s radius at around 6 371 kilometers (3 959 miles) in length is one fundamental aspect that underlies many scientific disciplines as well as practical applications. It is a value that assists navigation systems as well as promotes our knowledge concerning planets’ science among others; hence it forms an integral part of present life and scientific inquiry.